www.eprace.edu.pl » aproksymacja-wielomianami » Aproksymacja średniokwadratowa. » Aproksymacja wielomianami Legendre`a
Aproksymacja wielomianami Legendre`a
Funkcję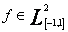 
( gdzie symbolem 
oznaczamy przestrzeń funkcji całkowalnych z kwadratem na [ a, b ], w której to przestrzeni wprowadzamy iloczyn skalarny) aproksymujemy jej sumę Fouriera
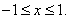(15)
Współczynniki 
obliczamy za pomocą wzorów
k = 0,1,2,...n. (16)
Zachodzi równość
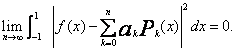(17)
Tw. 1.
Jeśli funkcja f ma w przedziale 
druga pochodną ciągłą, to jest ona rozwijalna w szereg jednostajnie zbieżny według wielomianów Legendre`a w tym przedziale.
Przykład 2. Obliczyć kilka współczynników aproksymacji funkcji 
w przedziale wielomianami Legendre`a.
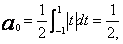
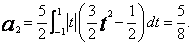(18)
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.